一、问题

如果有三个整数a，n，k，要让我们求出a^n的后k位，你会怎么求？

也许有人可能会想到直接将a^n次求出，然后通过取余求出后k位

但显然，这样是不现实的，因为我们知道当这个数很大时，即使是long long型的变量也存放不下。

二、前置知识

当我们解决问题之前，首先来看一下，我们需要了解的一些知识。

三、解决问题

解决一个问题的最好方法，往往是从实例中应用，所以我们不妨假设a = 3, n = 45
此外，如果计算机基础较好的读者很容易得到45 = (101101)2

于是，我们可以得到如下推导

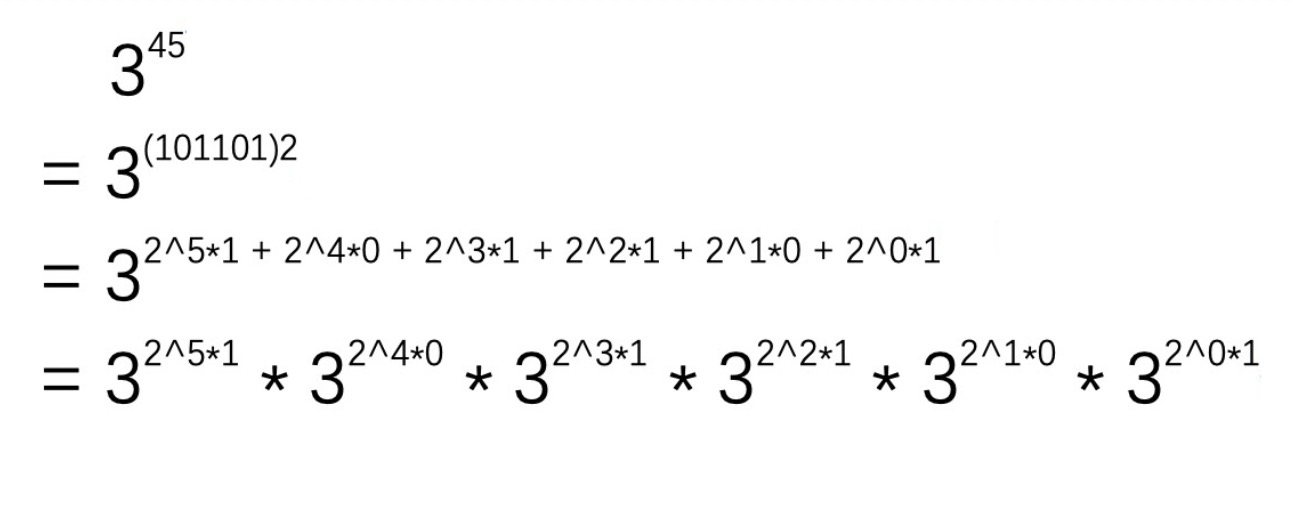
我们可以发现，如果最后一步中每一项去掉*后面的乘数，则每一项的值都为后一项的平方

四、代码实现

#include <iostream>
#include <cmath>

using namespace std;

int main() {
    int a, n, k;
    while(cin >> a >> n >> k) {
        int mod = pow(10, k);
        int ans = 1; // 先定义最终结果为1
        while (n) {
            if (n & 1) { // 判断n的二进制最后一位是0还是1
                ans = (ans * a) % mod; // 只有当二进制最后1位为1时，这一项底数才为a，否则为1
            }
            n >>= 1; // 二进制右移一位
            a = (a * a) % mod; // 如之前推导，前一项为后一项平方
        }
        cout << ans << endl;
    }
    return 0;
}